液压泥浆泵水动力学方法测试

液压泥浆泵工作原理是利用液压马达将液压能转换为机械动能后，带动叶轮使粘土、石块与水混合物负压抽取方式进行吸排作业。在其叶轮及壳体等设计成形后，应当进行水动学试验来验证叶轮及壳体的流向、扰流等现象来分析液压泥浆泵形成的稳定流、非稳定流以及层流与乱流的关系，逐渐改进液压泥浆泵的设计和优化生产流程。

所有的水流体包括泥浆，在某种程度上而言都遵循着的基本公理为守恒律，特别是质量守恒、动量守恒以及能量守恒。除此之外，水流体还假设遵守“连续性假设”。水流体从微观情况下来看是由分子所构成，彼比在运动过程中互相碰撞，也同样与砂石等颗粒固体相碰撞。因此，除了质量、动量与能量守恒方程之外，另外还应有热力学的状态方程，使得压力成为流体其他热力学变量的函数，而使问题得以被限定。

液压泥浆泵的水动学前期构建模型是以无粘性流体对于剪切变形没有抗拒能力和静止水流体不能承受剪应力，可以判断无粘性流体的剪应力为零，而正应力（即法向应力）PXX=PYY=PZZ=-P。P称为无粘性流体或静止流体的压力函数。

液压泥浆泵的水动力学试验的主要任务是研究泥浆液体的机械运动规律及其工程应用。具体来讲，就是研究泥浆液体的运动要素（如速度、加速度等）随时间和空间的变化情况，以及建立这些运动要素之间的关系式，并利用这些关系式来解决工程上所遇到的实际问题。

拉格朗日（Lagrange）法就是把液体运动看作是无数质点运动的总和，用以研究个别液体质点的运动为基础，通过研究足够多的液体质点的运动来掌握整个液流的运动情况。所以，这种方法又称为质点系法。

而欧拉法就是把液体的运动看作是各个空间点上不同液体质点运动情况的总和。我们从液压泥浆吸排的泥浆情况分析，是从物理概念角主角出发，认定流场是运动的液体质点占据整个流动区域构成的，因而流场空间点上反映出来的运动要素值及其随时间的变化当然是质点运动的结果。

我们可以依靠计算机辅助系统和三维物理动力状态下的液体流动模型建立泥浆的迹线与流线的模型方式。所谓的迹线就是指泥浆液体质点在吸作用下流动的过程中不同时刻所占据的空间位置的连线，而流线则是某一瞬时在流场中绘出的一条空间曲线，在曲线上所有质点在该时刻的流速矢量都与该曲线相切。液体的流线在同一瞬间的流线不能相交，也不能转折，只能是一条光滑的曲线，它代表着质点在液压泥浆泵的流动运动状态，流线分布的疏密程度反应流速的大小。

在泥浆流中任意取一微分面积，通过该面积周界上的每一点均可作出一条流线，这无数条流线组成的封闭的管状曲面就称为流管。

根据泥浆的水力要素与液压泥浆壳体内空间自变量的关系，水流分为一元流、二元流、三元流。在泥浆液体的流场中任一点的液体运动要求仅与一个空间自变量有关，这种水流称为一元流。相同的，如果与两个空间或三个空间自变量相关，则分别称为二元流和三元流。其中二元流被称为平面运动，三元流被称为空间运动。

先锋管道液压泥浆泵的专家们通过三元流动的方法，在计算机上实现了两类流面交迭代的方法已经实现，并用于泥浆泵叶轮的流动计算，与通常三元解不同的是还需对旋涡分离区-尾迹的形状作修正。正是由于这些原因才使得高效率的叶轮制造提供了理论依据。

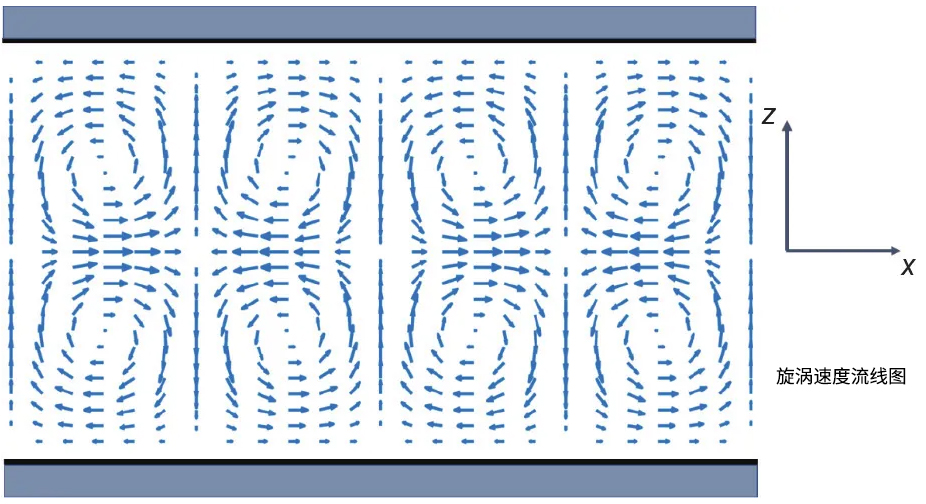
在实际的液压泥浆泵在运转中，泥浆流体具有粘性并且夹杂着砂粒和石块，其泥浆运动的复杂程度要高于纯水运动理论。因此，在水模型中加入杂质后发现，杂质的运动与水介质运动轨迹大致相同，但由于其密度较大，受到重力、浮力、相互碰撞及水流中涡流现象会损失一部分能量，且砂石在泥浆中所含比例是随机的，并随着泥浆泵吸排的过程不断变化。

总之，先锋管道液压泥浆泵数据模型已经构建出来，随着计算机模拟环境（包括水流、杂质及三元流）的建立和制造技术的不断完善，使其结构变得越来越简化和更加的实用化，尤其是管道工程和防汛抢险作业中，泥浆泵的流量、扬程会随着模型的计算而不断优化，复杂环境和条件下的工况都会随着模拟出来，而液压泥浆泵的各部件的计算会变得简单和容易。有时看着不同品牌而外表大概相同的两个泵体和内部结构，在实际工程应用以及测试中会有明显的差别，这就是不断优化的结果。

将在后续的文章中进行液压泥浆泵模型中介绍流函数、势函数等因素对泥浆泵实际运转中流速场和压强场的关系。

参考文献：

1.翟建华. 计算流体力学(CFD)的通用软件[J]. 河北科技大学学报, 2005, 26(2):6.

2.任玉新, 陈海昕. 计算流体力学基础[M]. 清华大学出版社, 2006.

3.罗榕婷, 张光辉, 曹颖. 坡面含沙水流水动力学特性研究进展[J]. 地理科学进展, 2009(4):8.

4.谭洪卫. 计算流体动力学在建筑环境工程上的应用[J]. 暖通空调, 1999, 29(4):6.